Математики

Евклид

Евклид был греческим математиком и также известен как отец геометрии. О нем известно очень немного и сохранилось очень мало оригинальных ссылок на Евклида, поэтому мало что известно о его жизни. Вероятно, он родился в 325 г. до н.э., хотя место и обстоятельства его рождения и смерти неизвестны и могут быть оценены только приблизительно относительно других людей, упомянутых с ним. Его главной работой является “Начала”  именно в этой работе Евклида был заложен фундамент современной математики в том виде в котором мы сейчас ее знаем. “Начала” выступали в качестве основного учебника для преподавания математики (особенно геометрии ) со времени ее публикации до конца 19-го века. Большая часть его работ вращалась вокруг теории чисел и геометрии. Он оказал наибольшее влияние на развитие математики.

Интересные сведения из истории возникновения математики

Откуда же взялась математика? Куда же уходит корнями история развития математики? Самым первым источником появления простейшей математики ученые считают пальцы на руках и ногах, а также различные части тела. Об этом свидетельствует множество наскальных рисунков, дошедших до нашего времени. Учеными установлено, что 6 тысяч лет назад древние вавилоняне уже использовали простые математические действия: для бытовых нужд, учета скота, подсчета количества урожая, размера прибыли и расходов, при совершении купли или продажи различных товаров. Позже они же первые упоминают о решении математических задач и уравнений повышенной сложности. К самым первым математическим открытиям относят возникновение математических действий, которые известны нам как сложение, вычитание, умножение и деление.

Ученые-историки до сих пор спорят о точной дате появления этой науки и о месте, где впервые она появилась. Конкурентами в этом споре выступают древний Вавилон и Египет. Самые первые подтверждения математической деятельности принадлежат Свазиленду. Там найдены кости бабуинов с нанесенными черточками, которые явно говорят о первых математических операциях, выполненных 40000 лет назад.

()

А когда же появились дроби? Упоминания о дробях возникли гораздо позже, но уже достоверно известно, что жители древнего Египта совершали операции с дробями, у которых числителем являлась единица.

А вот представление о десятичных дробях появилось всего лишь пять столетий назад, а в Европу попало только через 200 лет после появления.

 

 (И)

Невероятные факты, связанные с математикой:

• Всю математическую науку возможно записать в сто тысяч томов;
• Центилион – самое большое известное число, содержащее шестьсот нулей;
• Наименьшее число используется только в астрономии. Названия не имеет. Записывается дробью; после запятой имеет сто миллионов триллионов нулей, а в конце единицу;
• Самая магическая цифра, которая таит множество суеверий – 666. В Европейской палате все время пустует только одно кресло под номером 666. Во всем мире люди стараются не использовать это число. Такой номер не присваивается телефонным кодам, автобусам,трассам или поездам;
• В Китае самым суеверным числом считают число 4. При этом, такой номер не присваивается домам, квартирам, нет даже 4 этажа.

Математика очень дружна со всеми существующими науками, видами деятельности и профессиями. Одно мудрое выражение гласит «Математика-язык других наук». Поспорить с этим очень сложно, ведь она является основой для развития таких дисциплин:

• Химия;
• Физика;
• Астрономия;
• Биология;
• История;
• Экономика;
• География;
• Информатика;
• Политология;
• Музыка;
• Литература.

Теперь мы можем с уверенностью сказать, что знание математики – залог вашей успешности и развития не только в будущем, а уже сегодня!

Основные темы

Количество

Основной раздел, рассматривающий абстракцию количества — алгебра. Понятие «число» первоначально зародилось из арифметических представлений и относилось к натуральным числам. В дальнейшем оно, с помощью алгебры, было постепенно распространено на целые, рациональные, действительные, комплексные и другие числа.

1,2,…{\displaystyle 1,\;2,\;\ldots } Натуральные числа ,1,−1,…{\displaystyle 0,\;1,\;-1,\;\ldots } Целые числа 1,−1,12,23,,12,…{\displaystyle 1,\;-1,\;{\frac {1}{2}},\;{\frac {2}{3}},\;0{,}12,\;\ldots } Рациональные числа 1,−1,12,,12,π,2,…{\displaystyle 1,\;-1,\;{\frac {1}{2}},\;0{,}12,\;\pi ,\;{\sqrt {2}},\;\ldots } Вещественные числа
−1,12,,12,π,3i+2,eiπ3,…{\displaystyle -1,\;{\frac {1}{2}},\;0{,}12,\;\pi ,\;3i+2,\;e^{i\pi /3},\;\ldots }	1,i,j,k,πj−12k,…{\displaystyle 1,\;i,\;j,\;k,\;\pi j-{\frac {1}{2}}k,\;\dots }
Комплексные числа	Кватернионы

Числа — Натуральные числа — Целые числа — Рациональные числа — Иррациональные числа — Алгебраические числа — Трансцендентные числа — Вещественные числа — Комплексные числа — Гиперкомплексные числа — Кватернионы — Октонионы — Седенионы — Гиперреальные числа — Сюрреальные числа — p-адические числа — Математические постоянные — Названия чисел — Бесконечность — Базы

Преобразования

Явления преобразований и изменений в самом общем виде рассматривает анализ.

36÷9=4{\displaystyle 36\div 9=4}			∫1Sdμ=μ(S){\displaystyle \int 1_{S}\,d\mu =\mu (S)}
Арифметика	Дифференциальное и интегральное исчисление	Векторный анализ	Анализ
d2dx2y=ddxy+c{\displaystyle {\frac {d^{2}}{dx^{2}}}y={\frac {d}{dx}}y+c}
Дифференциальные уравнения	Динамические системы	Теория хаоса

Арифметика — Векторный анализ — Анализ — Теория меры — Дифференциальные уравнения — Динамические системы — Теория хаоса

Структуры

Теория множеств — Линейная алгебра — Общая алгебра (включает, в частности, теорию групп, универсальную алгебру, теорию категорий) — Алгебраическая геометрия — Теория чисел — Топология.

Пространственные отношения

Основы пространственных отношений рассматривает геометрия. Тригонометрия рассматривает свойства тригонометрических функций. Изучением геометрических объектов посредством математического анализа занимается дифференциальная геометрия. Свойства пространств, остающихся неизменными при непрерывных деформациях и само явление непрерывности изучает топология.

Геометрия	Тригонометрия	Дифференциальная геометрия	Топология	Фракталы	Теория меры

Геометрия — Тригонометрия — Алгебраическая геометрия — Топология — Дифференциальная геометрия — Алгебраическая топология — Линейная алгебра — Фракталы — Теория меры.

Дискретная математика

Дискретная математика включает средства исследования объектов, способных принимать только отдельные (дискретные) значения (то есть объектов, не способных изменяться плавно).

∀x(P(x)⇒P(x′)){\displaystyle \forall x(P(x)\Rightarrow P(x’))}
Математическая логика	Теория вычислимости	Криптография	Теория графов

Комбинаторика — Теория множеств — Теория решёток — Математическая логика — Теория вычислимости— Криптография — Теория функциональных систем — Теория графов — Теория алгоритмов — Логические исчисления
— Информатика.

Понятие числа. Виды чисел

В понятие числа входит обозначение количественного состава чего-либо.Это одно из главных определений в математике. Каждый вид числа появлялся в результате необходимости выполнения человеком тех или иных расчетов. В связи с необходимостью владеть информацией о количестве предметов, появилось понятие натурального числа и бесконечности ряда натуральных чисел. Необходимость измерения площадей, длин, объемов – породила рациональное число. Для решения сложных уравнений ввели комплексные числа.

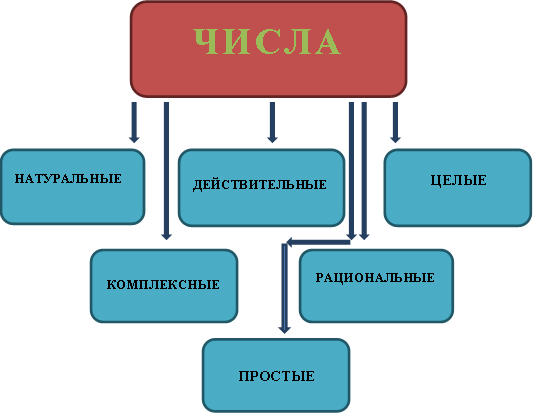
• Натуральные числа – это числа, получаемые при определении количества 1,2,3. Множество таких чисел принято обозначать буквой N. Например: 1,2,3 …..
• Целые числа. Определение понятия формулируется так: множество натуральных, отрицательных чисел и нуль. Их принято обозначать буквой Z. Например: -2,-1,0,1,2,3,4…..
• Рациональные числа. В понятие рационального числа входят дроби m/n, где n≠0, при этом m – целое число, а n – натуральное. Обозначаются буквой Q. Например: 2/3, -4/5
• Действительные. В понятие действительного числа включены рациональные и иррациональные числа, которые могут записываться в виде обычной и десятичной конечной и бесконечной дробей, а также нуль. Обозначаются буквой R. Например: 1245, 5⅔, -648,35
• Простыми называют натуральные числа, которые можно представить в виде двух множителей – единицы и самого этого числа. Обозначается буквой Р. Например: 1,3,7,11….
• Также существуют Иррациональные числа – это числа, не являющиеся рациональными, то есть нельзя представить в виде дроби m/n, где n≠0, при этом m – целое число, а n – натуральное. Например, число  пи=3,1415926535, число e=2.718281828, квадратный корень из 3 и так далее.

Отцы-основатели

За многие тысячелетия огромное количество учёных занимались развитием математических знаний

Кто-то из них снискал себе мировую славу, кто-то оказался не столь известен широкой публике, но тем не менее, сделал в математике что-то весьма важное. Список известных математиков состоит из многих десятков, если не сотен, фамилий

Мы упомянем лишь некоторых: тех, кто волею судьбы или благодаря своей гениальности оказался «на исторической сцене». И начнём с нескольких имён тех людей, кто жил и творил в глубокой древности, но заложил, таким образом, основы этой науки.

Эвклид

Этот учёный из Древней Греции жил примерно в III веке до нашей эры. Примерно, потому что мы мало знаем о его жизни, разве лишь то, что проживал он в Александрии. Да и то, некоторые источники, особенно арабские, утверждают, что на самом деле Эвклид был «прописан» в Дамаске.

Эвклида называют отцом геометрии. Он доказал много теорем и гипотез, написал несколько научных трактатов. Из них два труда — «Элементы» и «Начала», заложили базовый фундамент всей последующей европейской математики. В «Началах» содержится известная каждому школьнику теорема Пифагора. По этому учебнику преподавали геометрию в школах Европы около 2 тысяч лет!

Пифагор

Если Эвклид — отец геометрии, то Пифагора величают отцом математики. Он также жил в Греции, за полторы сотни лет до Эвклида. Создал собственную математическую школу, впервые в истории человечества сделал математику прикладной наукой, вводя её элементы в повседневный обиход. Кстати, далеко не все историки согласны с тем, что именно он доказал свою знаменитую тригонометрическую теорему.

Архимед

Древнегреческий учёный из Сиракуз занимался многими науками, но, по словам Плутарха, «был одержим математикой». Много работал в области геометрии, сам же считал своим главным достижением выведение формулы для исчисления площади шара и его объёма. Идеи Архимеда заложили основу интегрального исчисления.

Андрей Николаевич Колмогоров

Когда упоминаются великие математики России, одним из первых на ум приходит именно этот научный деятель.

Алексей Николаевич Колмогоров родился весной 1903 года в городе Тамбове. Начальное образование он получил дома, после чего поступил в частную гимназию. Уже там были отмечены его удивительные способности в области точных наук. В силу ряда обстоятельств его семья была вынуждена переехать в Москву, где их и застала Гражданская война. Несмотря ни на что, Колмогоров поступил в Московский университет на факультет математики. Успехи молодого студента на выбранном поприще были столь велики, что он без особых усилий смог досрочно сдать экзамены, не отрываясь от своего основного увлечения – теории вероятности. В научных изданиях стали появляться труды Андрея Николаевича, начиная с 1923 года, а ведь ему на тот момент едва минуло 20 лет. Методично добиваясь желаемого, математик уже в 1939 году стал академиком. Он проработал всю жизнь в Москве и умер осенью 1987 года, похоронен на Новодевичьем кладбище.

К его весомым работам можно отнести:

• Усовершенствование методики преподавания математики в начальных и средних школах. Великие математики и их открытия мирового масштаба важны, однако не менее ценной и нужной является работа по подготовке молодого поколения будущих научных деятелей. Всем известно, что основы закладываются в раннем детстве.
• Развитие математических методов и перенос их из абстрактных областей в прикладные. Иными словами, благодаря трудам Андрея Николаевича математика прочно вошла в естественные науки.
• Вывод принятых мировым научным сообществом аксиом элементарной теории вероятностей. Последняя характеризуется тем, что описывает конечное число событий.

Философия математики[править | править код]

Основная статья: Философия математики

Цели и методыправить | править код

Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного раздела математики — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.

Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.

Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. «Пространство , при является математической выдумкой. Впрочем, весьма гениальной выдумкой, которая помогает математически разбираться в сложных явлениях».

Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.

Основанияправить | править код

Вопрос сущности и оснований математики обсуждался со времён Платона. Начиная с XX века наблюдается сравнительное согласие в вопросе, что надлежит считать строгим математическим доказательством, однако отсутствует согласие в понимании того, что в математике считать изначально истинным. Отсюда вытекают разногласия как в вопросах аксиоматики и взаимосвязи отраслей математики, так и в выборе логических систем, которыми следует при доказательствах пользоваться.

Помимо скептического, известны нижеперечисленные подходы к данному вопросу.

Теоретико-множественный подходправить | править код

Основная статья: Теория множеств

Предлагается рассматривать все математические объекты в рамках теории множеств, чаще всего с аксиоматикой Цермело — Френкеля (хотя существует множество других, равносильных ей).
Данный подход считается с середины XX века преобладающим, однако в действительности большинство математических работ не ставят задач перевести свои утверждения строго на язык теории множеств, а оперируют понятиями и фактами, установленными в некоторых областях математики. Таким образом, если в теории множеств будет обнаружено противоречие, это не повлечёт за собой обесценивание большинства результатов.

Логицизмправить | править код

Основная статья: Логицизм

Данный подход предполагает строгую типизацию математических объектов. Многие парадоксы, избегаемые в теории множеств лишь путём специальных уловок, оказываются невозможными в принципе.

Формализмправить | править код

Основная статья: Формализм (математика)

Данный подход предполагает изучение формальных систем на основе классической логики.

Интуиционизмправить | править код

Основная статья: Интуиционизм

Интуиционизм предполагает в основании математики интуиционистскую логику, более ограниченную в средствах доказательства (но, как считается, и более надёжную). Интуиционизм отвергает доказательство от противного, многие неконструктивные доказательства становятся невозможными, а многие проблемы теории множеств — бессмысленными (неформализуемыми).

Конструктивная математикаправить | править код

Основная статья: Конструктивная математика

Конструктивная математика — близкое к интуиционизму течение в математике, изучающее конструктивные построения[прояснить]. Согласно критерию конструктивности — «существовать — значит быть построенным». Критерий конструктивности — более сильное требование, чем критерий непротиворечивости.

Российские математики

В заключение хотелось бы подчеркнуть, что свой вклад, причём значительный, внесли в европейскую математическую науку и российские учёные. Вспомним хотя бы о некоторых их них.

Николай Лобачевский (1792 — 1856 гг.)

Создал особый раздел в геометрии, до сих пор называемый неэвклидовой геометрией, или попросту, геометрией Лобачевского. Его труды, не признанные современниками, опередили своё время, изменили традиционное представление о пространстве и заложили фундамент для работ Эйнштейна. Также уточнил понятие непрерывной функции, разработал несколько остроумных теорем о тригонометрических рядах.

Софья Ковалевская (1850 — 1891 гг.)

Первая женщина в России, ставшая профессором математики. Много работала в области небесной механики и математической физики, описывала вращение твёрдого тела, решила одну из так называемых задач Коши.

Андрей Колмогоров (1903 — 1987 гг.) 

Один из тех учёных, кто разработал теорию вероятностей в её современном виде. В своих трудах добился фундаментальных результатов в функциональном анализе, теориях множеств, мере и приближение функций.

Великие математики и их открытия изменили знания людей о нашем мире, Вселенной, частью которой мы являемся. Благодаря их трудам мы получили возможность не просто созерцать окружающий мир, но просчитывать его, понимать механизмы его функционирования. Математика стала тем ключиком, которым люди научились открывать двери природы, пусть далеко не все. Но, зная математические законы, мы в определённой мере начали «читать» книгу Вселенной. Язык этой книги — математику, подарили человечеству, в том числе, и те люди, о которых мы только что прочитали.

Примечания[править | править код]

1. Государственный образовательный стандарт высшего профессионального образования. Специальность 01.01.00. «Математика». Квалификация — Математик. Москва, 2000 (Составлено под руководством О. Б. Лупанова)

Для улучшения этой статьи желательно?: Проверить достоверность указанной в статье информации. Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.

Википедия Разделы математики адрес Викисловарь — адрес Викицитатник — адрес Викиучебник — адрес Викитека — адрес Викиновости — адрес Викиверситет — адрес Викигид — адрес

Выделить Разделы математики и найти в: Вокруг света математики адрес Академик математики/ru/ru/ адрес Астронет адрес Элементы математики+&search адрес Научная Россия математики&mode=2&sort=2 адрес Кругосвет математики&results_per_page=10 адрес Научная Сеть Традиция — адрес Циклопедия — адрес Викизнание — математики адрес

Bing Yahoo Яндекс Mail.ru Рамблер Нигма.РФ Спутник Google Scholar Апорт Архив Интернета Научно-популярные фильмы на Яндексе Документальные фильмы

Список ru-вики Вики-сайты на русском языке Список крупных русскоязычных википроектов Каталог wiki-сайтов Русскоязычные wiki-проекты Викизнание:Каталог wiki-сайтов Научно-популярные сайты в Интернете Лучшие научные сайты на нашем портале Лучшие научно-популярные сайты Каталог научно-познавательных сайтов НАУКА В РУНЕТЕ: каталог научных и научно-популярных сайтов

• Страница – краткая статья
• Страница – энциклопедическая статья
• Разное – на страницах: , , ,

Софья Ковалевская

В январе 1850 года в Москве родилась девочка, в дальнейшем известная всему миру как женщина-математик – Софья Ковалевская. Именно она стала действующим членом Петербургской научной академии.

Она родилась в семье генерал-лейтенанта артиллерии В. В. Корвина-Круковского в родовом имении Палибино (Витебская губерния) и Елисаветы Федоровны Шуберт (в девичестве). Дед Ковалевской был математиком, а прадед занимался астрономическими исследованиями. Женщина-математик Ковалевская провела свои детские годы в Витебской губернии, с восьмилетнего возраста она получала уроки не только от гувернанток, но и от Иосифа Игнатьевича Малевича, сына мелкопоместного шляхтича.

Он неоднократно отмечал уникальные способности этой женщины. Математики России по праву гордятся Софьей, ее стремлением к объяснению сложных процессов и явлений.

В 1866 году Ковалевская побывала за границей, затем брала в Санкт-Петербурге математические уроки у А. Н. Страннолюбского. После замужества вместе с супругом Владимиром Онуфриевичем Ковалевским она отправилась за границу. Сначала Софья училась у Кенигсбергера в Гейдельбергском университете, затем ей посчастливилось стать ученицей К. Т. В. Вейерштрасса в Берлинском университете.

Как и многие другие женщины-математики, Софья не могла слушать лекции. Вейерштрасс, которого поразили ее математическими способностями, стал для нее куратором. Молодая женщин выступала за революционную борьбу, поддерживала теорию утопического социализма, поэтому в 1881 году вместе с мужем приехала в Париж, стала ухаживать за ранеными коммунарами. Она стала участницей операции по спасению из тюрьмы одного из деятелей Парижской Коммуны – В. Жаклара.

Многие известные женщины-математики жертвовали своей личной жизнью во имя «царицы наук», а Софье удавалось совмещать семью и науку.

Галилео Галилей

Этот научный деятель, проживший всю жизнь в Италии (с 1564 по 1642 год), знаком каждому школьнику. Период его деятельности пришелся на смутную пору, что проходила под знаком инквизиции. Любое инакомыслие каралось, наука преследовалась, так как противоречила утверждениям теологов. Никто и ничто не могло быть описано, ибо на все воля Божья.

Именно математик Галилей, согласно легенде, стал автором фразы «И всё-таки она вертится!», после того как отрекся от своих слов о том, что Земля вращается вокруг Солнца, а не наоборот. Шаг этот был обусловлен борьбою за жизнь, так как инквизиция сочла ересью его гипотезу, в которой участники вращения поменялись местами. Священнослужители не могли допустить того, чтобы Земля как творенье Божье перестала быть центром всего.

Однако его труды данной гипотезой не ограничились, ибо в историю он вошел как великий физик и математик. Галилей:

• путем эмпирических исследований отверг утверждение Аристотеля, в котором говорилась о том, что скорость падения тела прямо пропорциональна его весу;
• вывел парадокс имени себя, в котором количество натуральных чисел равно количеству их же квадратов, притом что большая часть чисел квадратами не является;
• написал труд «Рассуждение об игре в кости», в котором рассмотрел эталонную с точки зрения теории вероятностей задачу с выводом и обоснованием.

5 класс

• Математика 5 класс
  Самостоятельные и контрольные работы

  Авторы:

• Математика 5 класс

  Авторы:

• Математика 5 класс

  Авторы:

• Математика 5 класс

  Авторы:

• Математика 5 класс
  Арифметика. Геометрия.

  Авторы:

• Математика 5 класс

  Авторы:

• Математика 5 класс

  Авторы:

• Математика 5 класс
  Дидактические материалы

  Авторы:

• Математика 5 класс
  рабочая тетрадь

  Авторы:

• Математика 5 класс
  Рабочая тетрадь

  Авторы:

• Математика 5 класс
  рабочая тетрадь

  Авторы:

• Математика 5 класс
  сборник задач

  Авторы:

• Математика 5 класс

  Авторы:

• Математика 5 класс

  Авторы:

• Математика 5 класс

  Авторы:

• Математика 5 класс
  сборник задач и контрольных работ

  Авторы:

• Математика 5 класс
  рабочая тетрадь

  Авторы:

• Математика 5-6 класс
  сборник задач

  Авторы:

• Математика 5 класс

  Авторы:

• Математика 5 класс
  сборник задач и упражнений

  Авторы:

• Математика 5 класс
  контрольные работы

  Авторы:

• Математика 5 класс
  рабочая тетрадь

  Авторы:

• Математика 5 класс
  текущий итоговый контроль

  Авторы:

• Математика 5 класс
  дидактические материалы

  Авторы:

• Математика 5 класс
  тесты и самостоятельные работы

  Авторы:

• Математика 5 класс
  дидактические материалы

  Авторы:

• Математика 5 класс
  контрольные работы

  Авторы:

• Математика 5 класс

  Авторы:

Плюсы и минусы работы математиком

Плюсы:

• творческая работа, решение нестандартных задач;
• престижность;
• высокая зарплата в отдельных сферах;
• непрерывное саморазвитие и возможность построить карьеру в науке.

Минусы:

• высокий порог вхождения в профессию;
• высокие требования к знаниям и навыкам;
• сложное обучение.

Пройти обучение

Межрегиональная Академия промышленного и строительного комплекса (МАСПК) приглашает слушателей пройти обучение на курсах профессиональной переподготовки по направлению «Учитель математики». Ресурсы Академии позволяют дистанционно обучать тысячи специалистов из всех регионов России. Наши учебные программы составляются при участии ведущих специалистов в своей сфере и регулярно актуализируются, что позволяет нашим выпускникам успешно реализоваться в профессии.

Межрегиональная академия дополнительного профессионального образования (МАДПО) проводит регулярный набор на курсы дополнительного профессионального образования по специальности «Учитель математики». Мы предлагаем программы повышения квалификации в дистанционном формате по индивидуально согласованному графику, современную учебно-методическую базу и документы установленного образца по завершении обучения.

Национальная академия современных технологий (НАСТ) реализует программы дополнительного образования и приглашает специалистов пройти профессиональную переподготовку по направлению «Учитель математики». Учебные программы Академии предполагают задействование дистанционных технологий, что позволяет нашим слушателям получать образование без отрыва от основной деятельности в наиболее комфортном режиме.

Философские мысли

Отдельное внимание можно уделить книге, название которой в переводе на русский язык звучит как «Борьба за счастье. Две параллельные драмы

Сочинение С. К. и А. К. Леффлер». Произведение написано совместно со шведской писательницей Леффлер-Эдгрен, но оно пронизано идеями Ковалевской. В книге изображается судьба и развитие людей с разных точек зрения: «как оно было», «как оно могло быть».

Софья была убеждена в том, что все действия и поступки людей предопределены заранее, но она признавала и тот факт, что могут возникать такие моменты в жизни, когда появляются разные шансы. В таком случае у человека есть возможность выбрать свой путь, внести коррективы в судьбу, данную ему изначально.

Гипотеза, предложенная Ковалевской, основывалась на гипотезе Пуанкаре о дифференцированных уравнениях. Интегралы им рассматривались в качестве уравнений с несколькими неизвестными кривыми линиями, разветвляющимися лишь в части изолированных точек.

Теория Пуанкаре демонстрирует, что явление по кривой протекает до места бифуркации, но при этом невозможно предвидеть заранее, каков алгоритм последующего разветвления.

Леффлер отмечал, что Софья Ковалевская в ее воспоминаниях, рассматриваемых в «Киевском сборнике в помощь пострадавшим от неурожая», центральной фигурой видела себя. Те фразы, которые произносились главной героиней произведения, Алисой, взяты из подлинных высказываний женщины-математика. Драма повествует о всемогущей силе любви, требующей полной отдачи и самопожертвования. Именно так рассматривала данное чувство Софья Ковалевская, что мешало ей достичь простого женского счастья.

Эварист Галуа

Основатель высшей алгебры, которой пользуются наши современники, родился в 1811 году и пожил значительно меньше Лермонтова и Абеля. Однако Эварист Галуа успел сделать несколько фундаментальных открытий: от него мы знаем, что такое группа и поле в математике. Конечные поля носят его имя. Также он был республиканцем, революционером и дуэлянтом. Именно это и послужило причиной его смерти – Галуа был застрелен в 20-летнем возрасте. Судьба к этому человеку поистине была немилосердна, даже фильм “Невезучие” не смог бы проиллюстрировать его жизнь в достаточной мере.

Математикой начал заниматься случайно и поздновато – в 16 лет. Через год уже опубликовал первые исследования и открытия, но это не способствовало его успеху. Преподаватели не понимали и части того, что он делал. В Политехническую школу он по этой же причине не смог поступить трижды, каждый раз выходя из себя из-за непонимания его выкладок людьми, которые как раз математикой и занимаются. Второй провал случился вообще курьёзно: Галуа так рассердился, что бросил в экзаменатора тряпкой для протирки доски. Но потом всё-таки Политехническая школа сдалась под натиском гениального математика, и его приняли.

Математики Возрождения

После заката эллинической культуры математика Европы пережила несколько веков стагнации, пока новая плеяда умов не вдохнула в эту науку новые идеи. Назвать выдающихся математиков того времени намного сложнее, потому что их оказалось значительно больше, чем в Древней Греции.

Леонардо Пизанский

В европейской науке более известен как Фибоначчи. Жил и умер в городе Пиза (последняя треть XII – первая четверть XIII веков). Его отец, известный торговец, страстно хотел, чтобы сын продолжил семейное дело, поэтому брал юношу в далёкие поездки на Ближний Восток и даже в Северную Индию.

Здесь Леонардо познакомился с индийской и арабской математическими школами, которые в эти века значительно превосходили уровень европейской математики.

По возвращению в Европу написал ряд научных трудов, в том числе главный, по математике — «Книга абака». Леонардо ввёл в европейскую математику привычные нам арабские цифры, а также не менее привычную десятичную систему исчисления. Как истинный сын торговца, юноша внёс в математику понятие отрицательных чисел, называя их «долгом». Разработал основы бухгалтерского учёта.

Исаак Ньютон (1642 — 1727 гг.)

Выдающийся англичанин, классик физики, математики и астрономии. Среди нескольких его основных трудов есть один, касающийся математики, — «Математические начала натуральной философии». Это «Библия» классической механики, в которой приведены формулы для описания движения всех тел во Вселенной. Кроме того, Ньютон заложил основы дифференциального и интегрального исчислений.

Готфрид Лейбниц (1646 — 1716 гг.)

Этот немецкий учёный жил и творил в одно время с Ньютоном, и, независимо от последнего, создал основы математического анализа, опирающиеся на понятия бесконечно малых величин. Лейбниц представлял себе матанализ алгебраически, а не кинематически, как это делал Ньютон.

Леонард Эйлер (1707 — 1783 гг.)

В специальной литературе нередко можно встретить утверждение, что этот швейцарец является самым выдающимся математиком всех времён. Между прочим, он много лет прожил в России, в Петербурге, и даже многие свои работы написал на русском языке, который выучил в совершенстве всего за год!

Трудно найти отрасль математики, в которой Эйлер не написал бы хоть одну важную работу. Он впервые создал «математический оркестр», увязав множество доселе разрозненных дисциплин в единую систему математики. Язык современной математики нельзя представить без таких понятий, как «углы Эйлера» или «формула Эйлера». Некоторые математические вопросы до сегодняшнего дня преподают студентам «по Эйлеру».

Рене Декарт (1596 — 1650 гг.)

Когда мы говорили, что Ньютон и Лейбниц разработали основы математического анализа, справедливо было бы вспомнить, что их изыскания базировались не на пустом месте. Начальные идеи были известны ещё до работ этих учёных, а разработал их почти легендарный француз, Рене Декарт.

Современные математики считают его зачинателем аналитической геометрии. Он впервые ввёл понятия функции и переменной величины. С одним из достижений Декарта сталкивался практически каждый человек. Это система координат, известные всем шкалы «икс» и «игрек». Помимо этого, именно Рене ввёл в математику понятия гиперболы и параболы, овала и листа.

Жозеф Луи Лагранж (1736 — 1813 гг.)

В XVIII веке, наряду с Эйлером, этот француз считался лучшим европейским математиком. Был особенно силён в области математического синтеза. Разработал и доказал несколько важнейших теорем, в том числе «формулу конечных приращений».

Пьер-Симон Лаплас (1749 — 1827 гг.)

Много работал как астроном, но в математике известен как один из тех, кто разрабатывал теорию вероятностей. Специалистам известны уравнения его имени и преобразование Лапласа

Ввёл важное понятие математического ожидания

Иоганн Гаусс (1777 — 1855 гг.)

Мы говорили уже об отце математики — Пифагоре. А этого немца нередко называют королём математики. Гаусс написал ряд важнейших работ во многих отраслях этой науки, которые до сих пор остаются базовыми, классическими. Много работал в математическом анализе, в неэвклидовой геометрии, открыл так называемые «гауссовые числа», разработал модель комплексных чисел.