Ферма, Пьер

Научная деятельность

Когда Пьеру исполнилось 35 лет, он написал трактат «Введение к теории плоских и пространственных мест», где подробно изложил свое видение на аналитическую геометрию.

Великая теорема Ферма

В следующем году ученый сформулировал свою знаменитую «Великую теорему». Спустя 3 года он также сформулирует – Малую теорему Ферма.

Ферма вел переписку с самыми известными математиками, включая Мерсенна и Паскаля, с которым он дискутировал относительно теории вероятностей.

В 1637 г. разразилось знаменитое противостояние между Пьером и Рене Декартом. Первый в жесткой форме раскритиковал декартову «Диоптрику», а второй, дал разгромный отзыв на труды Ферма по анализу.

В скором времени Пьер не замедлил дать 2 верных решения – одно согласно статье Ферма, а другое – построенное на идеях «Геометрии» Декарта. В итоге стало очевидно, что метод Пьера оказался заметно проще.

Позже Декарт попросил прощения у своего оппонента, но до самой смерти относился к нему с предвзятостью.

Интересен факт, что открытия французского гения дошли до наших дней благодаря сборнику его крупной переписки с коллегами. Единственным его трудом на то время, изданным в печатном виде, был «Трактат о спрямлении».

Пьер Ферма раньше Ньютона сумел использовать дифференциальные методы для проведения касательных и вычисления площадей. И хотя он не систематизировал свои методы, сам Ньютон не отрицал того, что именно идеи Ферма подтолкнули его к разработке анализа.

Главной заслугой в научной биографии ученого принято считать создание теории чисел.

Ферма был чрезвычайно увлечен арифметическими задачами, которые нередко обсуждал с другими математиками. В частности, его интересовали задачи о магических квадратах и кубах, а также задания, связанные с закономерностями натуральных чисел.

Позже Пьер разработал метод систематического нахождения всех делителей числа и сформулировал теорему о возможности представления произвольного числа суммой не более 4-х квадратов.

Любопытно, что многие оригинальные методы решений задач и уровней, используемые Ферма, до сих пор остаются неизвестными. То есть ученый просто не оставил никаких сведений о том, как он решал то или иное задание.

Известен случай, когда Мерсенн попросил француза выяснить, является ли число 100 895 598 169 простым. Тот почти сразу сообщил, что данное число равняется 898423 умноженным на 112303, однако не рассказал, каким путем он пришел к такому выводу.

Выдающиеся достижения Ферма в области арифметики опережали свое время и были забыты на 70 лет, пока ими не увлекся Эйлер, опубликовавший систематическую теорию чисел.

Открытия Пьера бесспорно имели огромную значимость. Он разработал общий закон дифференцирования дробных степеней, сформулировал метод для проведения касательных к произвольной алгебраической кривой, а также описал принцип решения сложнейшей задачи нахождения длины произвольной кривой.

Ферма пошел дальше Декарта, когда захотел применить аналитическую геометрию к пространству. Ему удалось сформулировать основы теории вероятностей.

Пьер Ферма свободно владел 6 языками: французским, латинским, окситанским, греческим, итальянским и испанским.

НАШИ ЛЮДИ

Алена Полынь
Другое

парапсихолог, Председатель Союза ИСВ, Председатель ассоциации АСМ

Ylvis
Другое

комедийный норвежский дуэт из Бергена, состоящий из братьев Борда и Вегарда Илвисокера

XP Voodoo
Другое

один из родоначальников российского клубного, техно- и рейв движения

Wretch 32
Другое

английский репер и бывший грайм-мс из Тоттенэма, где он вырос сыном местного рэгги диджея

Wisin & Yandel
Другое

Хуан Луис Морера Луна и Льяндель Вегильa Малаве Саласар , взявшие себе творческие псевдонимы Wisin и Yandel

Timbuktu
Другое

«https://ru

TheHill88
Другое

YouTube-знаменитость, известная под ником TheHill88

The Doodler
Другое

Великая теорема Ферма

Рассуждения Ферма о натуральных числах были не единственными, и даже не Пифагор первым их обосновал. История исчислений натуральных чисел была известна еще в Шумере и Древней Индии, но только Пифагор записал эти рассуждения в современной математической формуле: x2 + y2 = z2, а Ферма увеличил количество неизвестных: xn + yn = zn.

Особый интерес к натуральным числам возродился в начале 17 столетия, после издания «Арифметики» Диофанта. Эта книга стала особо популярной среди ученых и философов, которые пытались рационально объяснить мироустройство, исключая всякое божественное начало. Среди них был и Пьер Ферма.

Во время чтения «Арифметики» ему в голову пришла идея заменить показатель степени 2 в теореме Пифагора любым другим числом. Тогда он понял: решения такому суждению не существует, и это можно доказать. Но само доказательство не записал из-за отсутствия места в книжке. На страницах книги II, обдумывая задачу 8, Ферма записал только следующее:

«Невозможно разложить куб на два куба, биквадрат на два биквадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него».

Доказать выдвинутое утверждение Ферма, что нет простого решения для уравнения, например, 32+42=52, когда n˃2, являющегося целым числом, впоследствии смогли немногие. Сегодня известно, что Ферма доказал отсутствие решения для n = 4. А из его переписки известно, что он также осуществил и доказательство для n = 3, но найти его среди писем не удалось.

Рассуждение Ферма о простых числах стало широко известным после того, как в 1670 году его сын Самюэль опубликовал книгу «Арифметика», но уже с комментариями отца. Путь доказательства занял более чем 350 лет. Сотни математиков пытались доказать утверждение Ферма, а получилось это лишь у Эндрю Уайлса в 1993 году.

Знаменательно, что очевидной практической ценности Великая теория Ферма не имеет. Но ее формулировка будоражила умы сотен математиков, что, в свою очередь, действительно приносило плоды в развитии теории математики. Помимо легендарной Великой (или «Последней», как ее еще называют) теоремы Ферма, не менее важную роль в развитии математики занимает другая теорема – малая.

Малая теорема Ферма – это еще одно знаменитое рассуждение, которое Ферма описал в письме к своему другу в 1640 году. Читается эта теорема так: если целое число п не делится на простое число р, то пр — 1—1 делится на число р.

Доказательство этой теоремы не заняло столько времени и усилий, как в случае с ее предшественницей, но ее роль в развитии математического мышления несомненно бесценна. Сегодня она является одной из самых важных теорем элементарной теории чисел, криптографии и современной алгебры.

Великая теорема Ферма

Ферма широко известен благодаря так называемой великой (или последней) теореме Ферма. Теорема была сформулирована им в 1637 году, на полях книги «Арифметика» Диофанта с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы привести его на полях.

Вероятнее всего, его доказательство не было верным, так как позднее он опубликовал доказательство только для случая {\displaystyle n=4} n=4. Доказательство, разработанное в 1994 году Эндрю Уайлсом, содержит 129 страниц и опубликовано в журнале «Annals of Mathematics» в 1995 году.

Простота формулировки этой теоремы привлекла много математиков-любителей, так называемых ферматистов. Даже и после решения Уайлса во все академии наук идут письма с «доказательствами» великой теоремы Ферма.

Ранние этапы

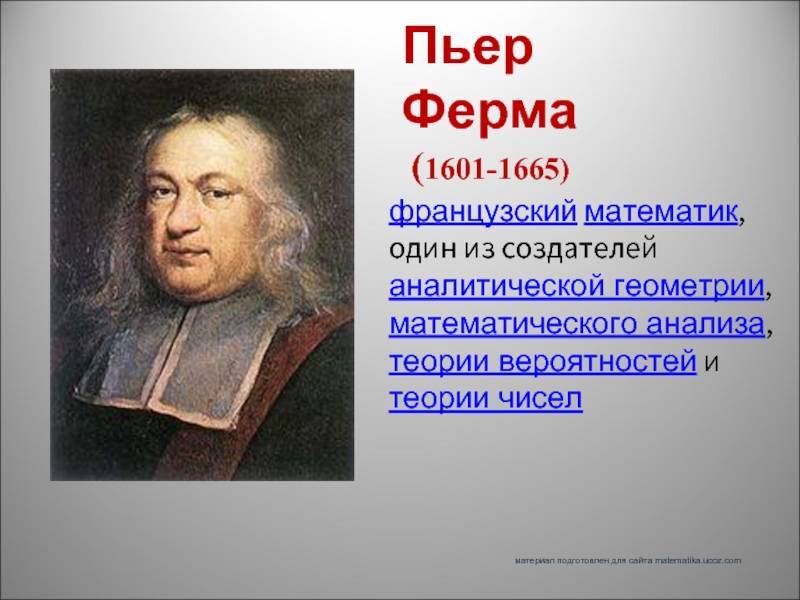
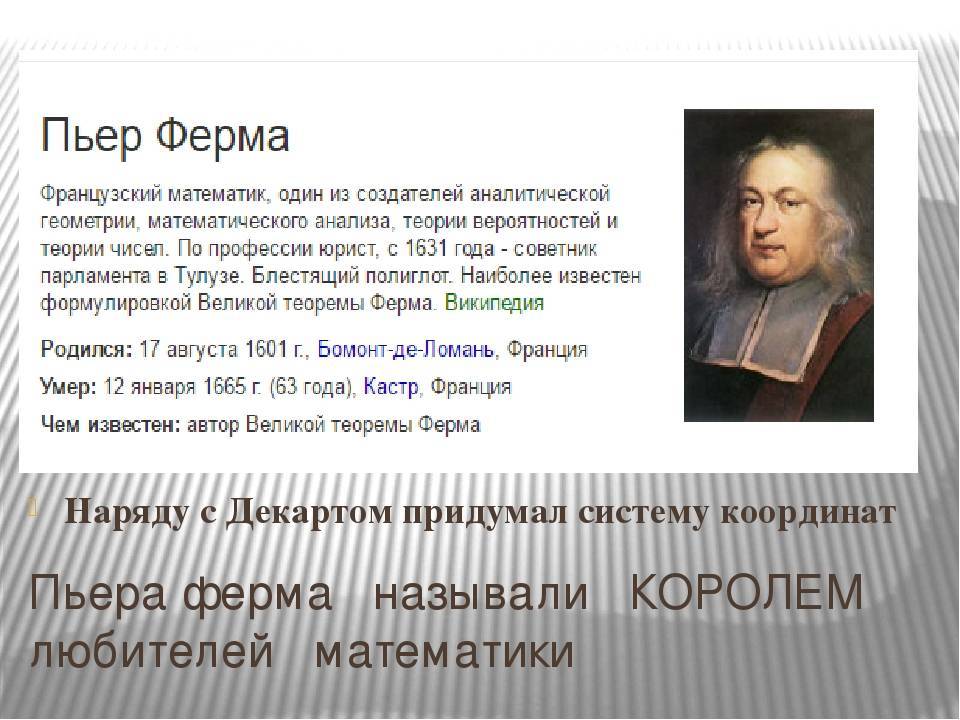
Пьер был рожден во Франции. Он является одним из первооткрывателей и создателей теории чисел, а также аналитической геометрии.

Длительное время говорили, что Пьер Ферма был рожден в 1595 году в Тулузе, но к середине девятнадцатого века в городе Бомоне в архивах была обнаружена запись, в которой было сказано, что летом 1601 года у советника города Доминика Ферма и его супруги появился на свет сын Пьер. Известно, что Доминик Ферма был очень уважаемым человеком в городе. Он был торговцем кожей. Детские годы Пьер провел рядом с родителями, а когда пришло время получать образование, он уехал в Тулузу – самый ближний город с университетами. Хорошенько изученное право на скамье университета дало Пьеру возможность работать адвокатом, но юноша решил перейти на службу к государству. В 1631 году Пьер был зачислен на место советника касс в парламент Тулузы. В это время Ферма уже был в браке с дочерью советника парламента, в котором он работал. Его жизнь была очень тихой и спокойной. Но благодаря ему сегодня люди, изучающие математику, могут почерпнуть для себя много интереснейшей информации, которая поистине бесценна

Даже в школьной программе активно уделяется внимание теме «Пьер Ферма и его открытия»

Полемика с Декартом

В 1637-38 годы французский математик Пьер Ферма бурным образом полемизировал с не менее выдающимся математиком Рене Декартом. Полемика возникала вокруг «Метода нахождения минимумов и максимумов». Декарт не до конца разобрался в методе и не понял его, по этой причине он подверг его несправедливой критике. Летом 1638 года Пьер Ферма посылает Мерсенну для передачи Декарту обновленное и более насыщенное подробностями изложение своего метода. В его письме отражается его сдержанный характер, потому что оно написано в крайне сухой и спокойной манере, но в то же время в нём есть некоторая доля иронии. В его письме содержится даже прямая насмешка над недопониманием Декарта. Ферма ни разу не вошел в бессмысленную и несдержанную полемику, он постоянно придерживался ровного и холодного тона. Это был не спор, а, скорее, беседа походила на общение преподавателя со студентом, который что-то не понял.

Другие достижения

Независимо от Паскаля Ферма разработал основы теории вероятностей. Именно с переписки Ферма и Паскаля (1654), в которой они, в частности, пришли к понятию математического ожидания и теоремам сложения и умножения вероятностей, отсчитывает свою историю эта замечательная наука. Результаты Ферма и Паскаля были приведены в книге Гюйгенса «О расчётах в азартной игре» (1657), первом руководстве по теории вероятностей.

Имя Ферма носит основной принцип геометрической оптики, в силу которого свет в неоднородной среде выбирает путь, занимающий наименьшее время (впрочем, Ферма считал, что скорость света бесконечна, и формулировал принцип более туманно). С этого тезиса начинается история главного закона физики — принципа наименьшего действия.

Биография

Пьер Ферма родился 17 августа года в гасконском городке Бомон-де-Ломань (Beaumont-de-Lomagne, Франция). Его отец, Доминик Ферма, был зажиточным торговцем-кожевником, вторым городским консулом. В семье, кроме Пьера, были ещё один сын и две дочери. Ферма получил юридическое образование — сначала в Тулузе (1620—1625), а затем в Бордо и Орлеане (1625—1631).

В 1631 году, успешно закончив обучение, Ферма выкупил должность королевского советника парламента (другими словами, члена высшего суда) в Тулузе. В этом же году он женился на дальней родственнице матери, Луизе де Лонг. У них было пятеро детей.

Памятник Ферма в Бомон-де-Ломань.

Быстрый служебный рост позволил Ферма стать членом Палаты эдиктов в городе Кастр (1648). Именно этой должности он обязан добавлением к своему имени признака знатности — частицы de; с этого времени он становится Пьером де Ферма.

Спокойная размеренная жизнь провинциального юриста оставляла Ферма время на самообразование и математические исследования. В 1636 году он написал трактат «Введение к теории плоских и пространственных мест», где независимо от «Геометрии» Декарта (вышедшей годом позже) изложил аналитическую геометрию. В 1637 году сформулировал свою «Великую теорему». В 1640 году обнародовал менее знаменитую, но гораздо более фундаментальную Малую теорему Ферма. Вёл активную переписку (через Марена Мерсенна) с крупными математиками того периода. С его переписки с Паскалем начинается формирование идей теории вероятностей.

В 1637 году начался конфликт Ферма и Декарта. Ферма уничтожающе отозвался о декартовой «Диоптрике», Декарт не остался в долгу, дал разгромный отзыв на работы Ферма по анализу и намекнул, что часть результатов Ферма являются плагиатом из декартовской «Геометрии». Метод Ферма для проведения касательных Декарт не понял (изложение в статье Ферма в самом деле было кратким и небрежным) и в качестве вызова предложил автору найти касательную к кривой, позднее названной «декартов лист». Ферма не замедлил дать два правильных решения — одно согласно статье Ферма, другое — основанное на идеях «Геометрии» Декарта, причём стало очевидным, что способ Ферма проще и удобнее. Посредником в споре выступил Жерар Дезарг — он признал, что метод Ферма универсален и правилен по существу, но изложен неясно и неполно. Декарт принёс извинения сопернику, но до конца жизни относился к Ферма недоброжелательно.

Около 1652 года Ферма пришлось опровергать сообщение о своей кончине во время эпидемии чумы; он действительно заразился, но выжил, причём смерть множества коллег продвинула Ферма до поста высшего парламентского судьи. В 1654 году Ферма совершил единственное в своей жизни дальнее путешествие по Европе. В 1660 году планировалась его встреча с Паскалем, но из-за плохого здоровья обоих учёных встреча не состоялась.

Пьер де Ферма умер 12 января 1665 года в городе Кастр, во время выездной сессии суда. Первоначально его похоронили там же, в Кастре, но позднее (1675) прах перенесли в семейную усыпальницу Ферма в тулузской церкви августинцев. В годы Французской революции останки Ферма затерялись.

Старший сын учёного, Клеман-Самуэль (также любитель математики), издал в 1670 году посмертное собрание трудов отца (несколько сотен писем и заметок), из которого научная общественность и узнала о замечательных открытиях Пьера Ферма. Дополнительно он опубликовал «Комментарии к Диофанту», сделанные отцом на полях перевода книги Диофанта; с этого момента начинается известность «Великой теоремы Ферма».

Современники характеризуют Ферма как честного, аккуратного, уравновешенного и приветливого человека, блестяще эрудированного как в математике, так и в гуманитарных науках, знатока многих древних и живых языков, на которых он писал неплохие стихи.

Увековечение памяти[править | править код]

Памятник Ферма в Бомон-де-Ломань.

• В 1935 г. Международный астрономический союз присвоил имя Пьера Ферма кратеру на видимой стороне Луны.
• Математическая премия Ферма вручается с 1989 года.
• В Тулузе имя Ферма присвоено улице, а также старейшему и самому престижному лицею Тулузы (Lycée Pierre de Fermat).
• В Бомон-де-Ломани, где родился Ферма, открыт его музей и установлен памятник учёному. В его честь названы улица и расположенный на этой улице отель.
• В честь Ферма названы различные математические теоремы и понятия, в том числе:

Великая теорема Ферма

Малая теорема Ферма

Метод факторизации Ферма

Проблема Штейнера

Спираль Ферма

Точка Ферма

Числа Ферма

Научная деятельность

Когда Пьеру исполнилось 35 лет, он написал трактат «Введение к теории плоских и пространственных мест», где подробно изложил свое видение на аналитическую геометрию.

Великая теорема Ферма

В следующем году ученый сформулировал свою знаменитую «Великую теорему». Спустя 3 года он также сформулирует – Малую теорему Ферма.

Ферма вел переписку с самыми известными математиками, включая Мерсенна и Паскаля, с которым он дискутировал относительно теории вероятностей.

В 1637 г. разразилось знаменитое противостояние между Пьером и Рене Декартом. Первый в жесткой форме раскритиковал декартову «Диоптрику», а второй, дал разгромный отзыв на труды Ферма по анализу.

В скором времени Пьер не замедлил дать 2 верных решения – одно согласно статье Ферма, а другое – построенное на идеях «Геометрии» Декарта. В итоге стало очевидно, что метод Пьера оказался заметно проще.

Позже Декарт попросил прощения у своего оппонента, но до самой смерти относился к нему с предвзятостью.

Интересен факт, что открытия французского гения дошли до наших дней благодаря сборнику его крупной переписки с коллегами. Единственным его трудом на то время, изданным в печатном виде, был «Трактат о спрямлении».

Пьер Ферма раньше Ньютона сумел использовать дифференциальные методы для проведения касательных и вычисления площадей. И хотя он не систематизировал свои методы, сам Ньютон не отрицал того, что именно идеи Ферма подтолкнули его к разработке анализа.

Главной заслугой в научной биографии ученого принято считать создание теории чисел.

Ферма был чрезвычайно увлечен арифметическими задачами, которые нередко обсуждал с другими математиками. В частности, его интересовали задачи о магических квадратах и кубах, а также задания, связанные с закономерностями натуральных чисел.

Позже Пьер разработал метод систематического нахождения всех делителей числа и сформулировал теорему о возможности представления произвольного числа суммой не более 4-х квадратов.

Любопытно, что многие оригинальные методы решений задач и уровней, используемые Ферма, до сих пор остаются неизвестными. То есть ученый просто не оставил никаких сведений о том, как он решал то или иное задание.

Известен случай, когда Мерсенн попросил француза выяснить, является ли число 100 895 598 169 простым. Тот почти сразу сообщил, что данное число равняется 898423 умноженным на 112303, однако не рассказал, каким путем он пришел к такому выводу.

Выдающиеся достижения Ферма в области арифметики опережали свое время и были забыты на 70 лет, пока ими не увлекся Эйлер, опубликовавший систематическую теорию чисел.

Открытия Пьера бесспорно имели огромную значимость. Он разработал общий закон дифференцирования дробных степеней, сформулировал метод для проведения касательных к произвольной алгебраической кривой, а также описал принцип решения сложнейшей задачи нахождения длины произвольной кривой.

Ферма пошел дальше Декарта, когда захотел применить аналитическую геометрию к пространству. Ему удалось сформулировать основы теории вероятностей.

Пьер Ферма свободно владел 6 языками: французским, латинским, окситанским, греческим, итальянским и испанским.

Примечания

1. , с. 15.
2. ↑ Стиллвелл Д. Математика и её история. — Москва-Ижевск: Институт компьютерных исследований, 2004, стр. 211—212.
3. , с. 124—128.
4. , с. 40.
5. , с. 58.
6. ↑ Вавилов С. И. Исаак Ньютон. 2-е дополненное издание. М.-Л.: Изд. АН СССР, 1945 г., глава 13.
7. Матвиевская Г. П. Учение о числе на средневековом Ближнем и Среднем Востоке. — Ташкент: ФАН, 1967. — С. 22—23. — 344 с..
8. Виленкин Н. Я. Популярная комбинаторика. — М.: Наука, 1975. — С. 10—11. — 208 с.
9. , с. 91.
10. Барабанов О. О., Барабанова Л. П. Алгоритмы решения навигационной разностно-дальномерной задачи — от Аполлония до Коши // История науки и техники, 2008, № 11, С.2-21.

Есть ли смысл?

Многие могут засомневаться в перспективности этого вида бизнеса. По словам Бориса Акимова, основателя кооператива LavkaLavka, их компания также пробовала реализовать проект вертикальных грядок в городе. Но производственные мощности оказались слишком малы (30 грядок для выращивания помидоров), чтобы получить с них доход.

Также есть печальный опыт проекта «I-Огород», в рамках которого основатели арендовали в Подмосковье теплицу, поставили веб-камеры. Они предлагали снять часть земельного участка и наблюдать за выращиванием на нем овощных культур. В итоге проект провалился.

Не созрело общество по состоянию на 2010 год и к агротуризму, поэтому те, кто тогда пробовал внедрить эту идею, скорее негативно настроены против «Телефермы». Они не верят в ее успех, считая, что бизнесмены не смогут привлечь достаточное количество клиентов для получения стабильного дохода.

Но некоторые существующие фермеры-горожане, которые уже сейчас держат скот на «Телеферме», строят амбициозные планы. Так, Юрий Нечаев обзавелся свиньей и 2 бычками. Он не планирует их отдавать на убой, хочет покрыть свинью, чтобы она дала помет. Это позволит расширить количество стада интенсивным методом. Также он выражает желание выкупить часть земли, построить на ней колбасный и пельменный цех, организовать полноценную собственную ферму. Для своих потенциальных партнеров г-н Нечаев готов построить взлетно-посадочную полосу (село расположено в 520 км от Мурома). Он подсчитал, что ему необходимы достаточно небольшие инвестиции (около 2-3 млн руб.)

Короткая предыстория

«Телефермер» – это стартап двух молодых людей Владислава Павлова и Михаила Химина, инвестировать в который согласился отец одного из них Дмитрий Павлов. Друзья вдохновились идеей Кимбала Маска Square Roots. Это вертикальные огороды, которые выращиваются внутри помещения, грядки на них размещаются вертикально. Но создавать такой комплекс в Москве они не рискнули. Их привлекла другая идея британской компании My Farm, она заключается в том, что городским жителям предлагается купить часть земли и удаленно управлять выращиванием на ней овощей и фруктов, получая свежий урожай к столу.

Павлов-старший, являясь соучредителем согласился вложить деньги в это направление. Он как раз размышлял, как привлечь сына к бизнесу, который не интересуется его компанией.

Как это работает?

Сумма стартовых инвестиций составила около 14 млн руб. Эти деньги пошли на покупку 60 га земли в Навашинском районе Нижегородской области, строительство дома, скотного двора, подвод коммуникаций, заработную плату персонала. В первый год было посажено несколько культур, из которых прижился только топинамбур. Поэтому от идеи продавать землю под огороды пришлось отказаться на начальном этапе.

Бизнесмены решили сосредоточиться на фермерстве. Клиентам предлагается купить животное, вкладывать деньги в корм для него и уход. Мясо можно есть самому или продавать. «Телефермер» получает свой комиссионный доход от предоставляемых услуг. Но партнеры не просто приглашают городских фермеров, они предлагают вступить в кооператив. Это не только облегчает ведение хозяйства, сбыт продукции, но и имеет ряд преимуществ в плане налогообложения.

На сегодняшний день клиентами компании стали 25 человек. Они купили поросят, баранов, бычков, кур. За своими животными городские фермеры наблюдают через веб-камеры. Также они могут нажать кнопку в приложении, чтобы покормить живность. Сигнал поступает на ферму, скотник выполняет поручение. Но этой возможностью не злоупотребляют, так как существует строгий график кормлений.

Чтобы стать клиентом, предусмотрена следующая процедура:

• Следует вступить в кооператив, созданный «Телефермером». Для этого оплачивается символический взнос 10 рублей.
• На счет заносятся деньги, которые снимаются для покупки скота и птицы, ухода за ними.

Клиенты самостоятельно решают, как быть с животными, дают соответствующие распоряжения. Свинью, овцу, птицу можно вырастить на убой, а мясо съесть самому, продать членам кооператива или отдать указание отвезти на пункт приема. В случае коммерческой деятельности нужно оплатить налог в размере 6%. Если в сделке участвуют члены кооператива, такие операции не являются объектами налогообложения.

Литература

• Башмакова И. Г. Диофант и Ферма (к истории метода касательных и экстремумов). Историко-математические исследования, 17, 1966, с. 185—207.
• Башмакова И. Г., Славутин Е. И. История диофантова анализа от Диофанта до Ферма. М.: Наука, 1984.
• Белл Э. Т. Творцы математики. – www.math.ru/lib/i/417/index.djvu?djvuopts&page=56 М.: Просвещение, 1979. Глава 4: Ферма.
• Ван дер Варден Б. Л. Переписка между Паскалем и Ферма по вопросам теории вероятностей. ИМИ, 21, 1976, с. 228—232.
• История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука, 1970. Том 2: Математика XVII столетия. – ilib.mccme.ru/djvu/istoria/istmat2.htm
• Ферма – ru.wikisource.org/wiki/ЭСБЕ/Ферма // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
• Фрейман Л. С. Ферма, Торричелли, Роберваль. В кн.: У истоков классической науки. М.: Наука, 1968, с. 173—254.
• Шаль. Исторический обзор происхождения и развития геометрических методов – ru.wikisource.org/wiki/Исторический_обзор_происхождения_и_развития_геометрических_методов/Ферма/ДО. Гл. 2, § 10-14. М., 1883.

Задача спрямления кривых

Одним из самых первых начал изучение задачи на вычисление длин дуг кривых. Ему удалось подвести решение задачи к нахождению некоторых площадей. К вычислению площади сводились все задачи на кривые. Оставалась одна капля для того, чтобы ввести новое и более абстрактное понятие «интеграл».

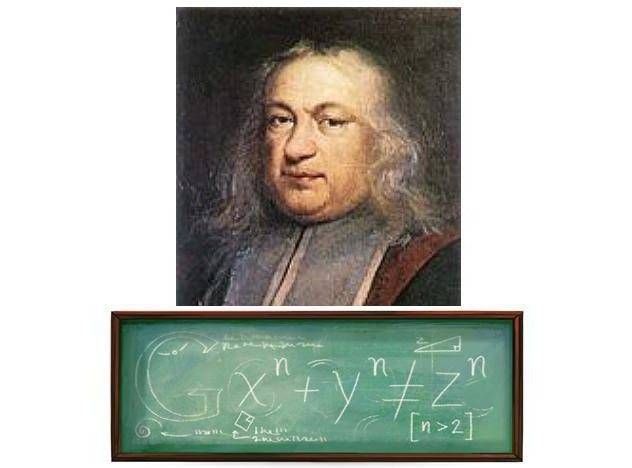
В дальнейшем весь положительный исход способов по определению «площадей» был в поиске взаимосвязи с «методом экстремумов и касательных». Есть сведения, что Ферма уже видел четкую взаимосвязь, но ни один из его трудов не отражает этой точки зрения.

В отличие от большинства своих сотоварищей по делу, Пьер де Ферма являлся чистейшим математиком и никогда не пытался исследовать другие отрасли науки. Вероятно, именно по этой причине его мощнейший вклад во всю математику настолько глубок и велик.

Наиболее распространенные виды хозяйств

Таким образом, ответ на вопрос о том, что такое ферма, понятен. Это частное предприятие, поставляющее на рынок сельхозпродукцию разных типов.

Конечно же, у нас в стране есть в том числе и растениеводческие КФХ. Однако зерновые и овощи в России чаще всего выращивают все же всевозможные сельскохозяйственные организации — товарищества, холдинги, ООО или ОАО. Фермеры у нас в стране в отрасли растениеводства занимаются в основном лишь возделыванием винограда и поставками на рынок грибов.

В большинстве же случаев в РФ КФХ специализируются все же на животноводстве. То есть выращивают КРС, МРС, свиней или птицу. Есть в России и множество КФХ:

звероводческих (кролики, нутрии, норки и пр);

пчеловодческих.

Увлечение историей

В юности будущий математик славился как тончайший знаток истории (в особенности античности), за его помощью обращались при издании классики Греции. Он оставил комментарии к трудам Синезуга, Атенея, Полюнуса, Фронтина, Теона Смирнского, внес правки в тексты Секста Эмпирика. Многие считают, что он с легкостью мог бы оставить свой след как выдающийся греческий филолог.

Однако благодаря тому, что он избрал иной путь, свет увидели его грандиозные по своей величине исследования. И поэтому большинство людей знает, что Пьер Ферма – математик.

О работах его при жизни в основном становилось известно посредствам широкой переписки, которую Ферма вел с иными учеными. Сборник сочинений, который он не единожды пробовал составить, так и не был претворен в жизнь. Собственно говоря, это логичный итог при такой загруженности на основной работе в суде. При жизни Пьера ни одно из массы его сочинений не было опубликовано.

Теорема Ферма

Конечно же, больше всего из трудов Пьера выделяется его великая и могучая теорема. Она многие годы и даже десятилетия заставляла «ломать головы» величайших математиков, и даже после того как она была опубликована в 1995 году, новые и очень разнообразные методы ее доказательств все еще поступают на кафедры с математическим уклоном во многие университеты мира.

Хотя Ферма оставил только краткие изложения своих трудов и обрывочную информацию, именно его открытия дали толчок многим другим выдающимся гениям математики. В его честь назвали один из наиболее престижных и старых лицеев во Франции – Лицей имени Пьера Ферма в Тулузе.

Теория чисел

Математики Древней Греции со времён Пифагора собирали и доказывали разнообразные утверждения, относящиеся к натуральным числам (например, методы построения всех пифагоровых троек, метод построения совершенных чисел и т. п.). Диофант Александрийский (III век н. э.) в своей «Арифметике» рассматривал многочисленные задачи о решении в рациональных числах алгебраических уравнений с несколькими неизвестными (ныне диофантовыми принято называть уравнения, которые требуется решить в целых числах). Эта книга (не полностью) стала известна в Европе в XVI веке, а в 1621 году она была издана во Франции и стала настольной книгой Ферма.

Ферма постоянно интересовался арифметическими задачами, обменивался сложными задачами с современниками. Например, в своём письме, получившем название «Второго вызова математикам» (февраль 1657), он предложил найти общее правило решения уравнения Пелля {\displaystyle ax^{2}+1=y^{2}} ax^{2}+1=y^{2} в целых числах. В письме он предлагал найти решения при a=149, 109, 433. Полное решение задачи Ферма было найдено лишь в 1759 году Эйлером.

Начал Ферма с задач про магические квадраты и кубы, но постепенно переключился на закономерности натуральных чисел — арифметические теоремы. Несомненно влияние Диофанта на Ферма, и символично, что он записывает свои удивительные открытия на полях «Арифметики».

Ферма обнаружил, что если a не делится на простое число p, то число {\displaystyle a^{p-1}-1} a^{p-1} – 1 всегда делится на p (см. Малая теорема Ферма)

Позднее Эйлер дал доказательство и обобщение этого важного результата: см. Теорема Эйлера

Обнаружив, что число {\displaystyle 2^{2^{k}}+1} 2^{2^k}+1 простое при k ≤ 4, Ферма решил, что эти числа простые при всех k, но Эйлер впоследствии показал, что при k=5 имеется делитель 641. До сих пор неизвестно, конечно или бесконечно множество простых чисел Ферма.

Эйлер доказал (1749) ещё одну гипотезу Ферма (сам Ферма редко приводил доказательства своих утверждений): простые числа вида 4k+1 представляются в виде суммы квадратов (5=4+1; 13=9+4), причём единственным способом, а для чисел, содержащих в своём разложении на простые множители простые числа вида 4k+3 в нечётной степени, такое представление невозможно. Эйлеру это доказательство стоило 7 лет трудов; сам Ферма доказывал эту теорему косвенно, изобретённым им индуктивным «методом бесконечного спуска». Этот метод был опубликован только в 1879 году; впрочем, Эйлер восстановил суть метода по нескольким замечаниям в письмах Ферма и неоднократно успешно его применял. Позже усовершенствованную версию метода применяли Пуанкаре и Андре Вейль.

Ферма разработал способ систематического нахождения всех делителей числа, сформулировал теорему о возможности представления произвольного числа суммой не более четырёх квадратов (теорема Лагранжа о сумме четырёх квадратов). Самое знаменитое его утверждение — «Великая теорема Ферма» (см. ниже).

Многие остроумные методы, применяемые Ферма, остались неизвестными. Однажды Мерсенн попросил Ферма выяснить, является ли многозначное число 100 895 598 169 простым. Ферма не замедлил сообщить, что {\displaystyle 100895598169=898423\cdot 112303;} {\displaystyle 100895598169=898423\cdot 112303;} он не пояснил, как нашёл эти делители.

Многие арифметические открытия Ферма опередили время и были забыты на 70 лет, пока ими не заинтересовался Эйлер, опубликовавший систематическую теорию чисел. Одна из причин этого — интересы большинства математиков переключились на математический анализ.